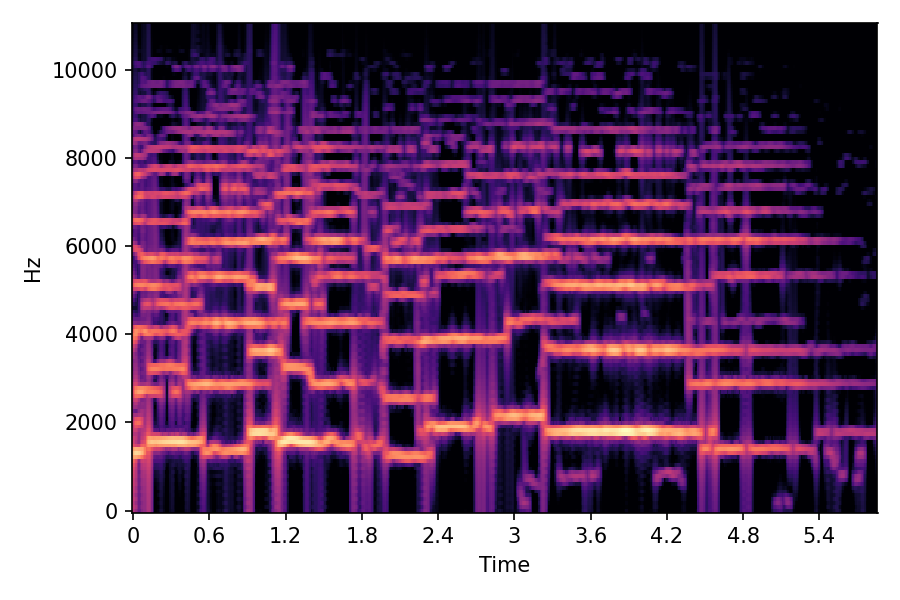
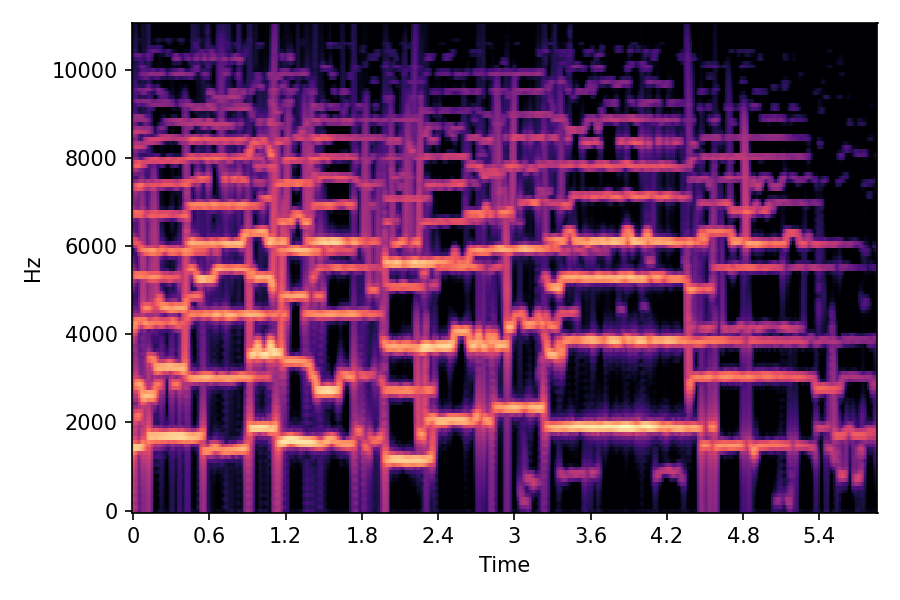
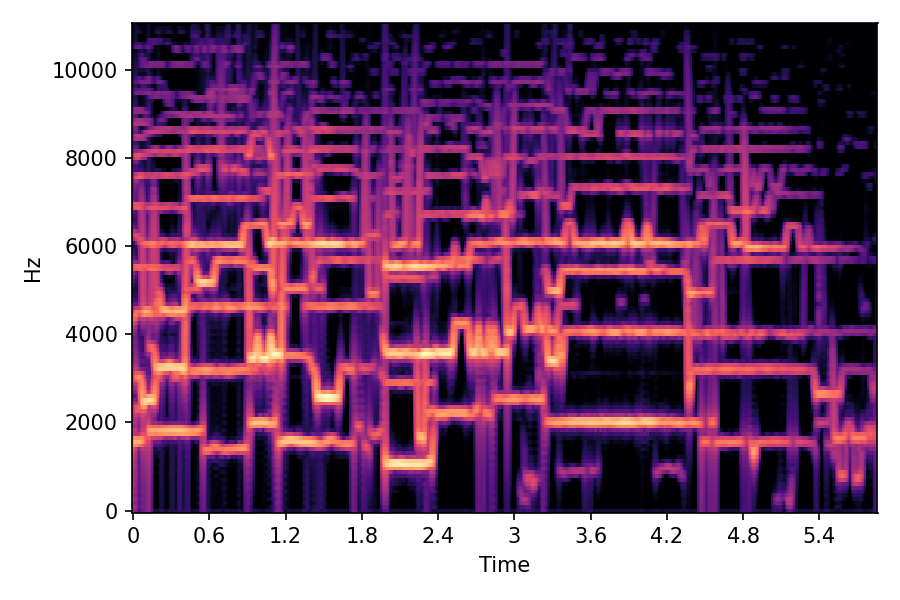
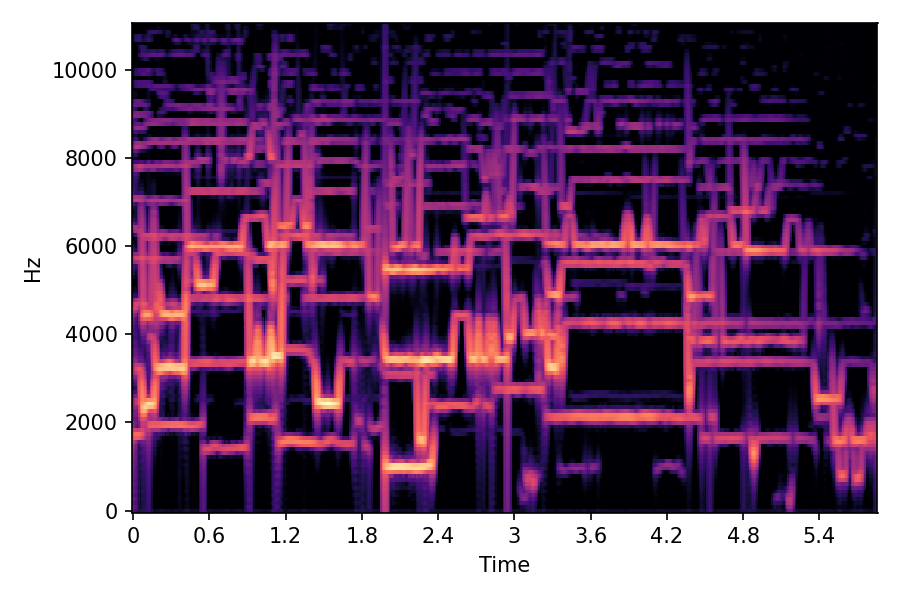
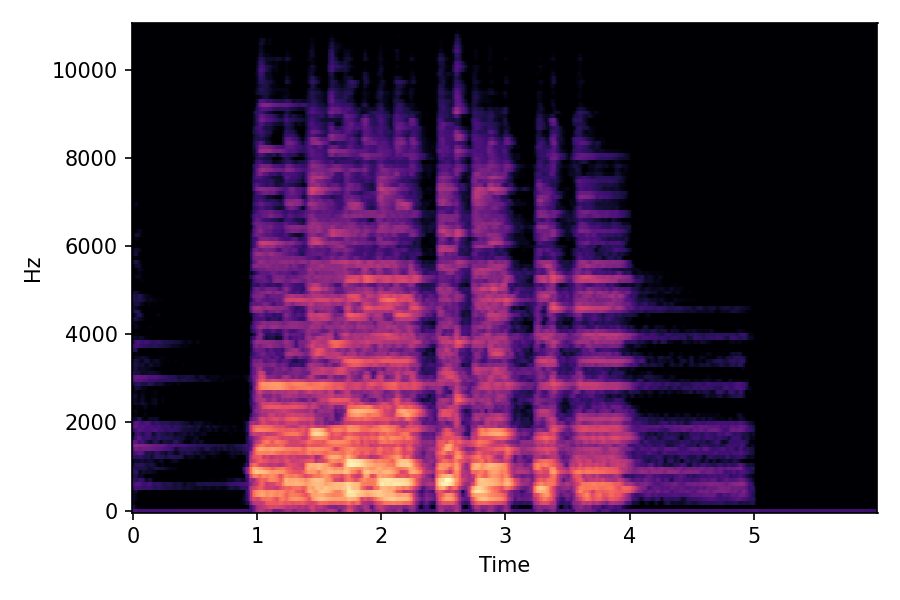
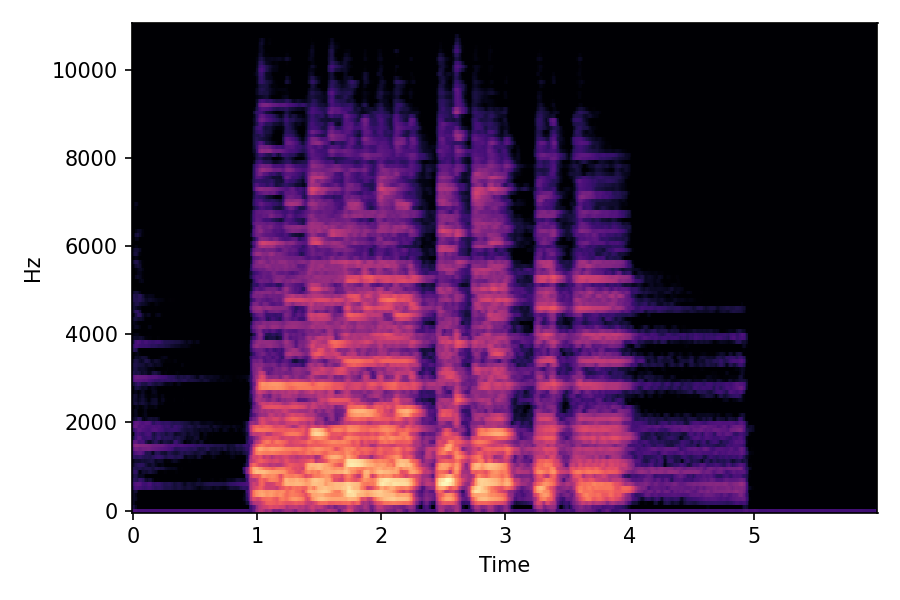
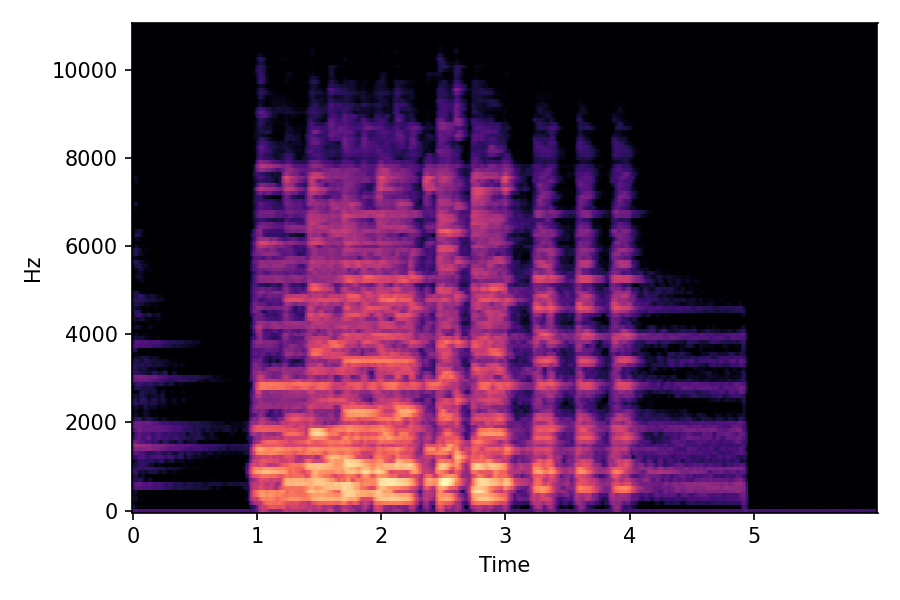
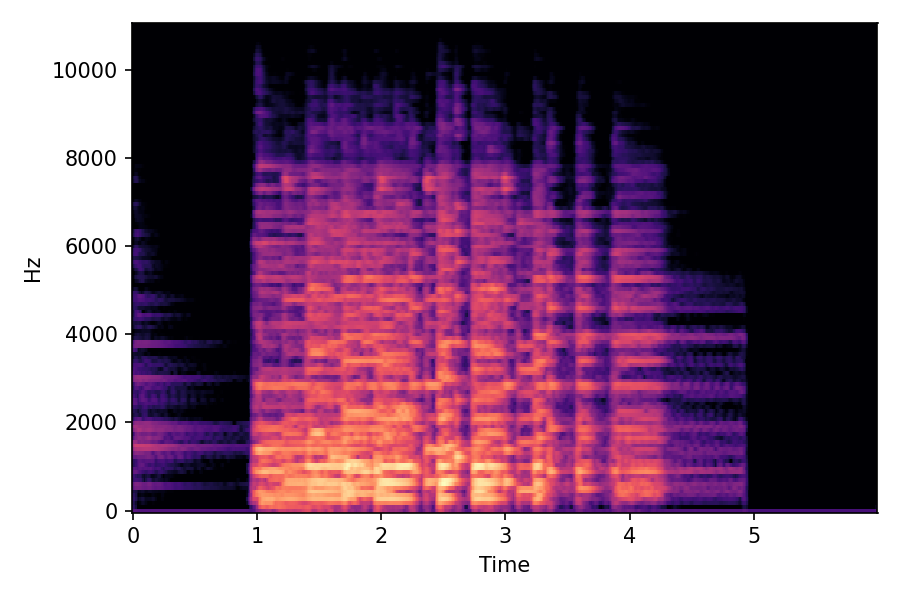
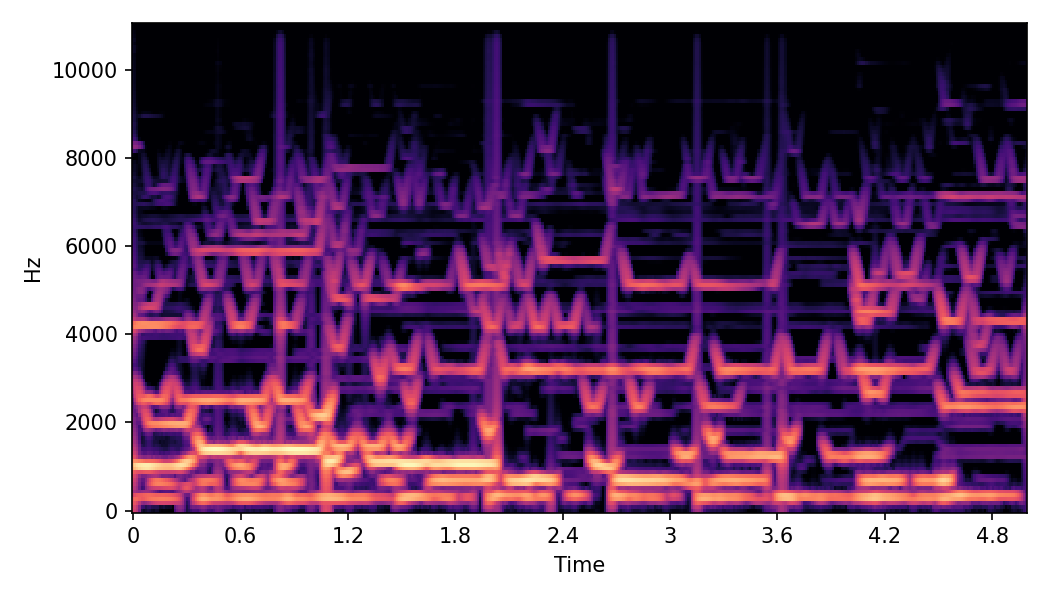
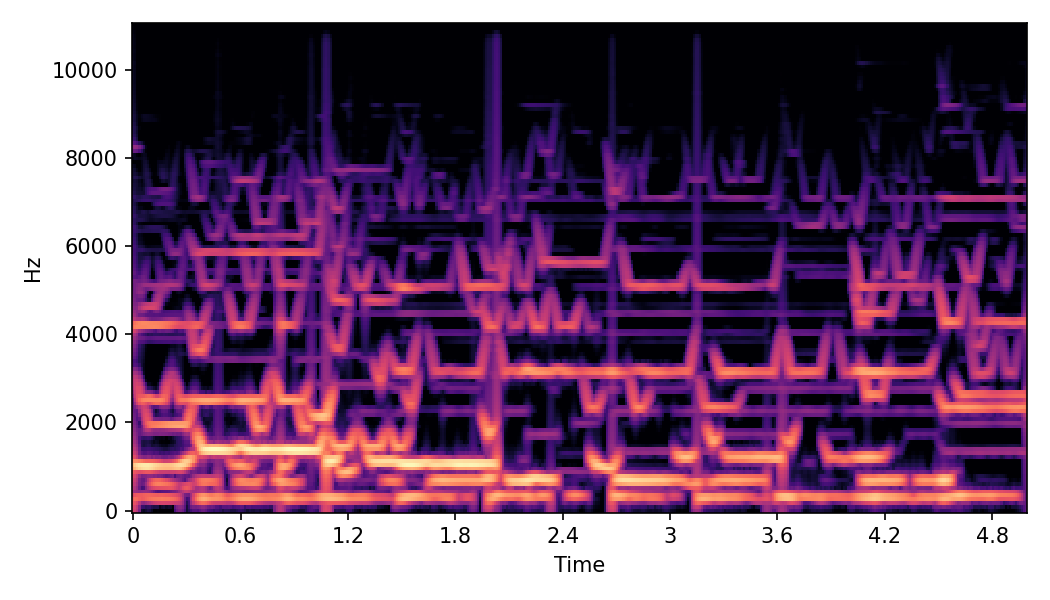
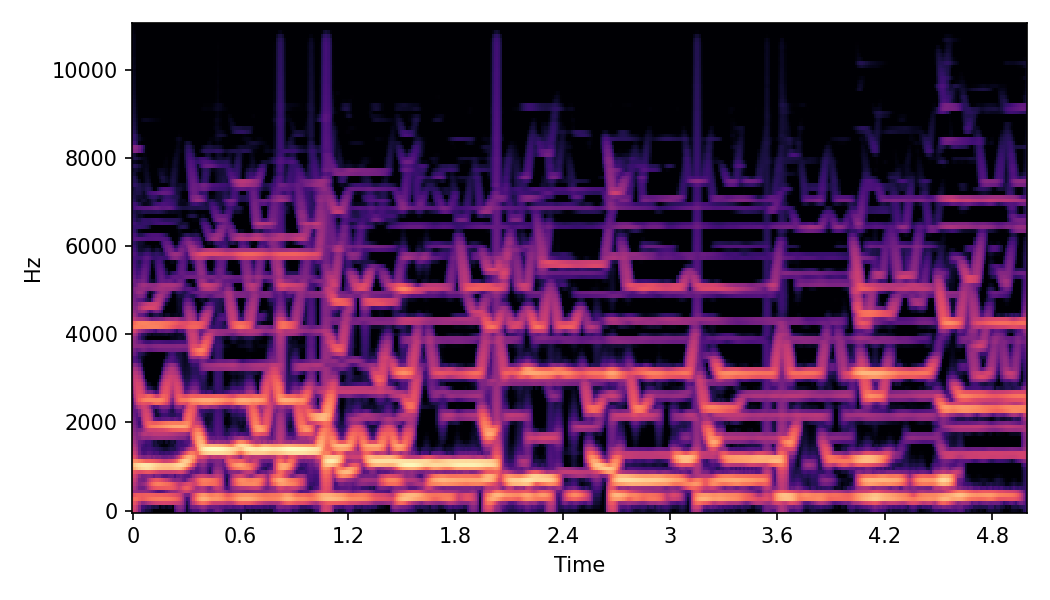
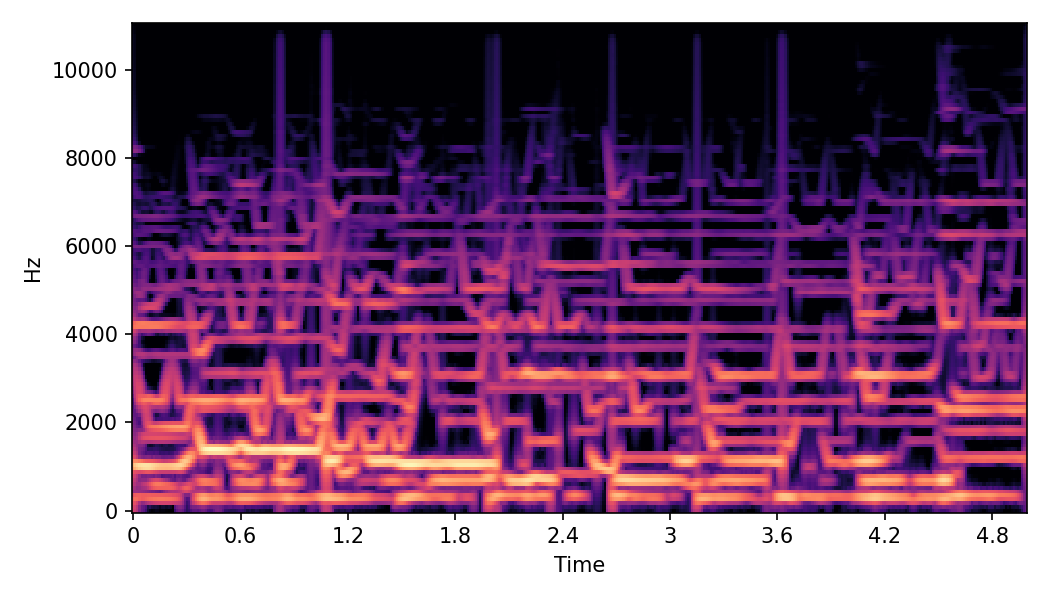
SoundMorpher: Perceptually-Uniform Sound Morphing with Diffusion Model

Return index page

Timbre Morphing

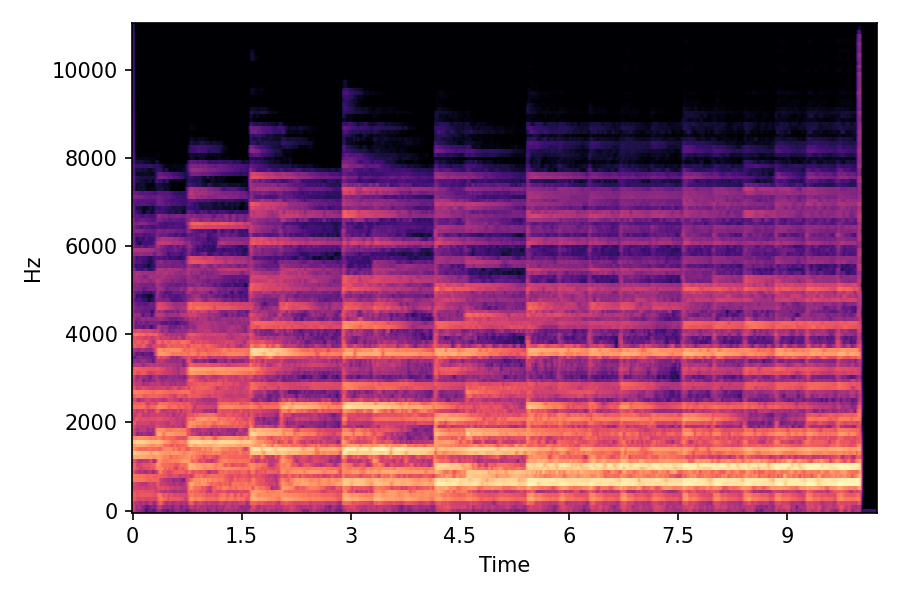
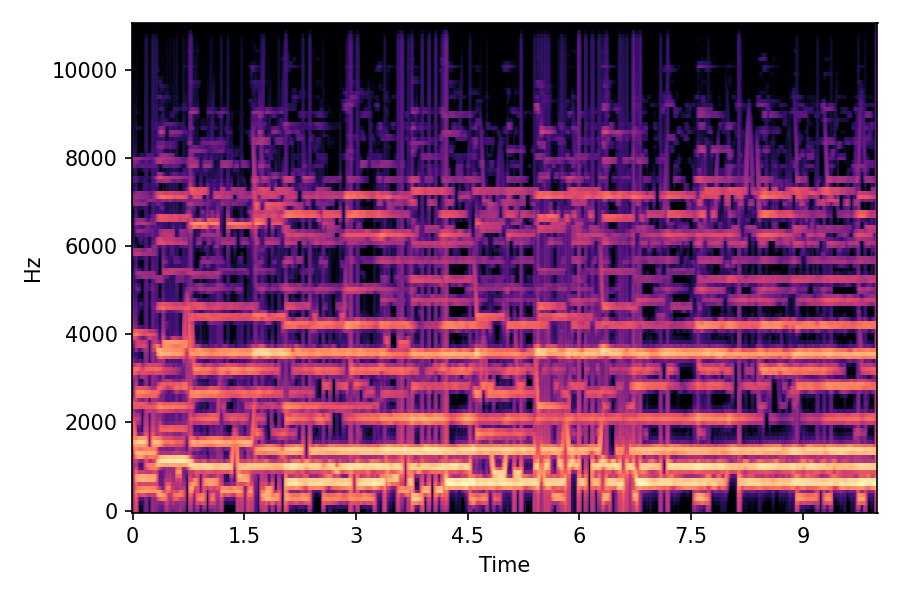
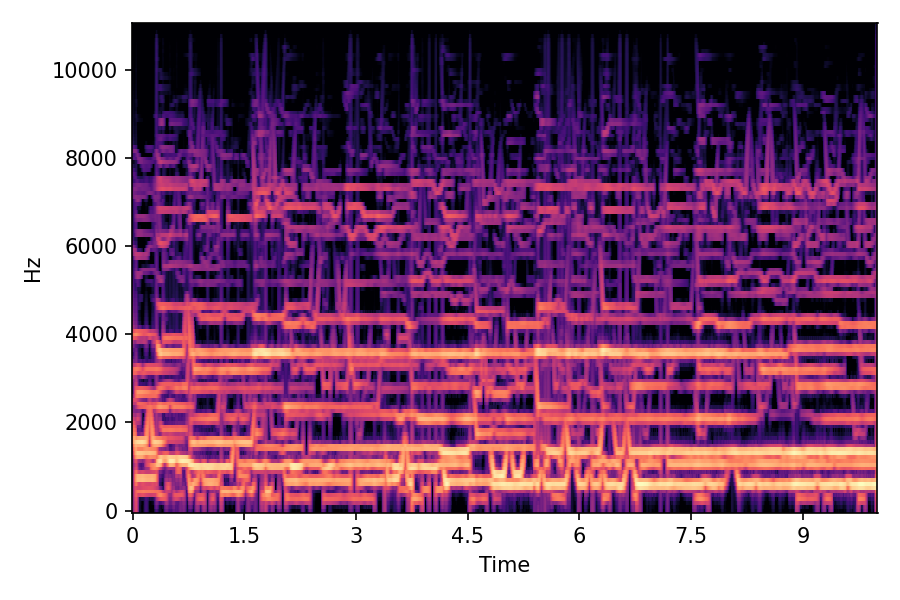
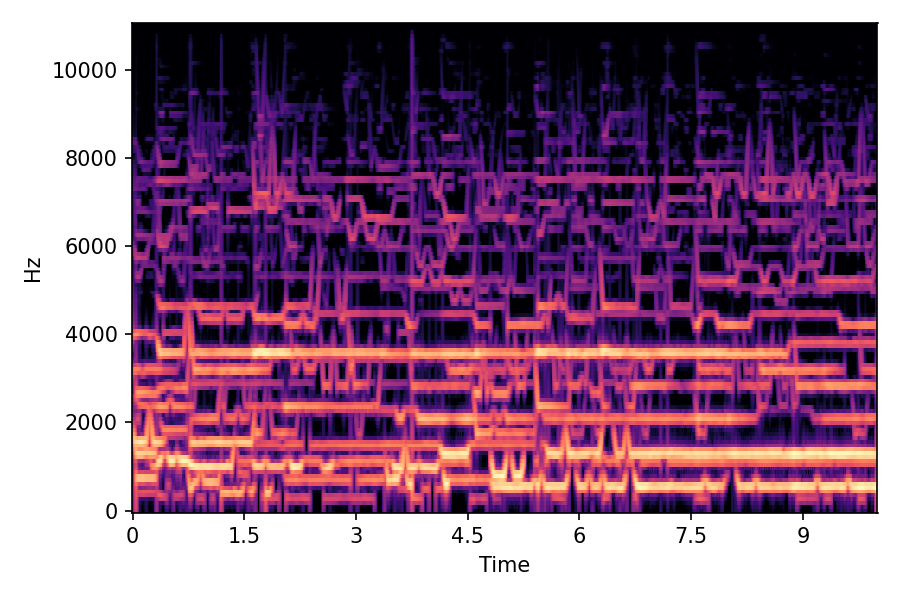
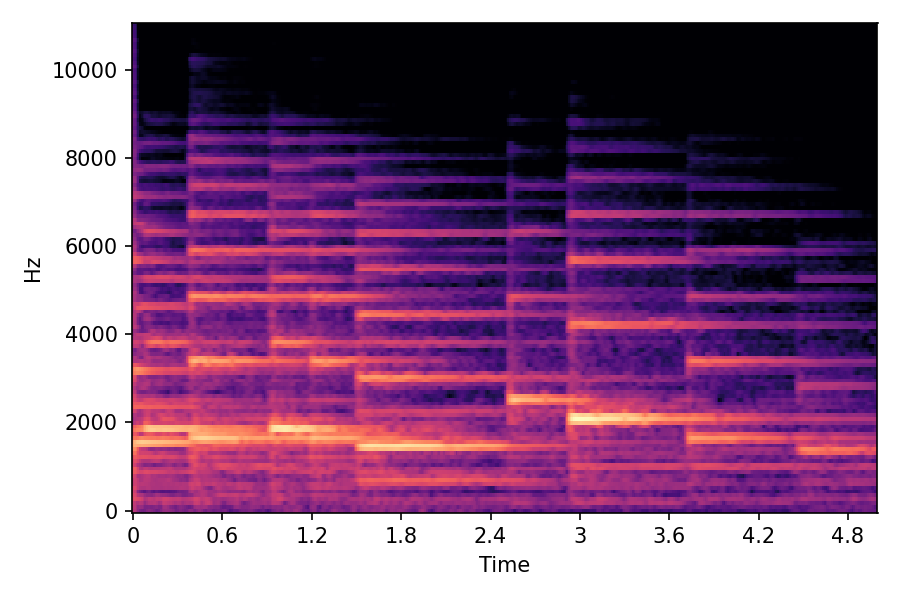
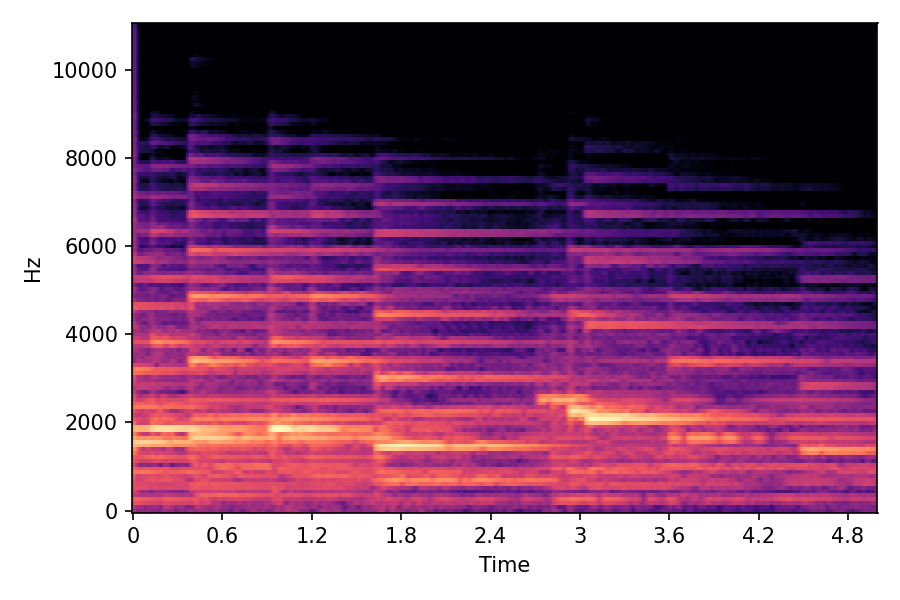
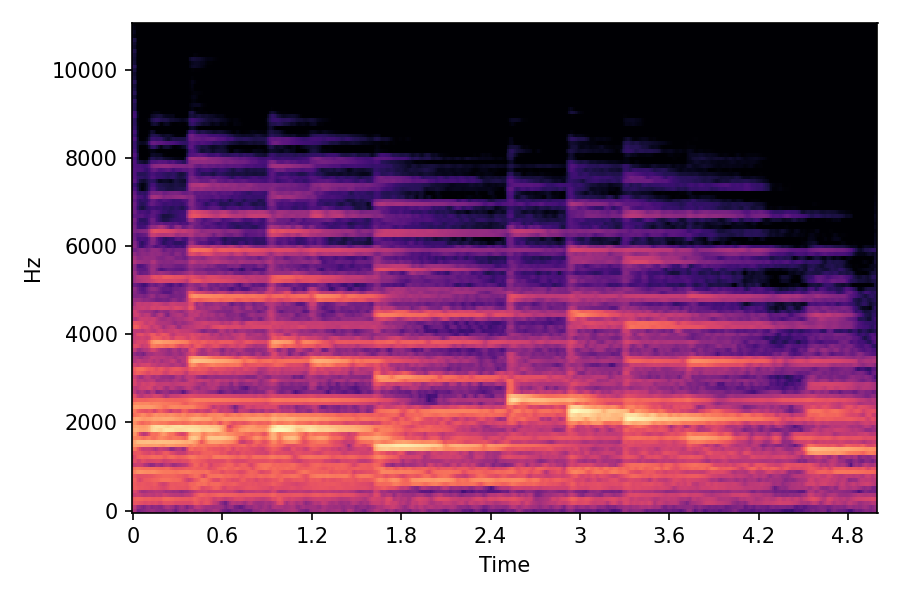
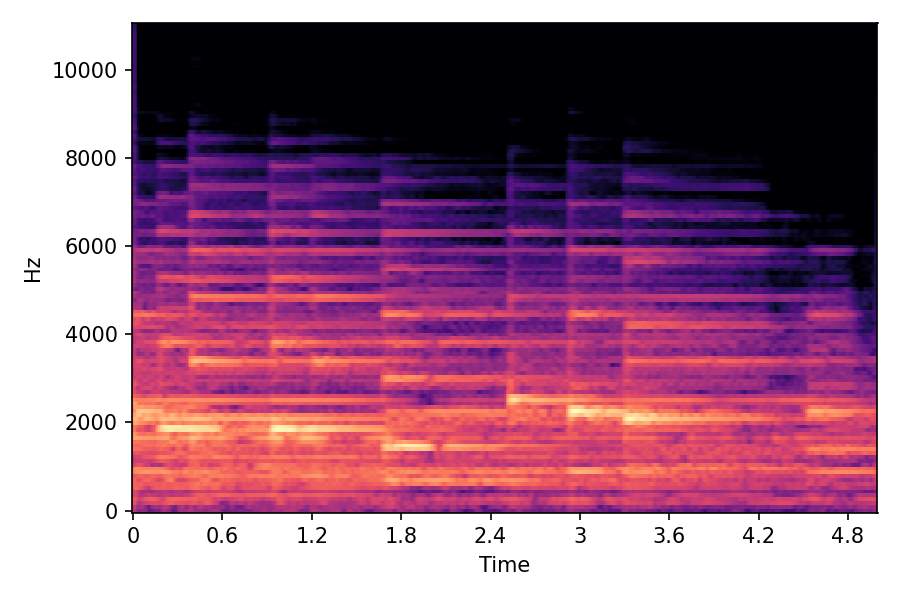
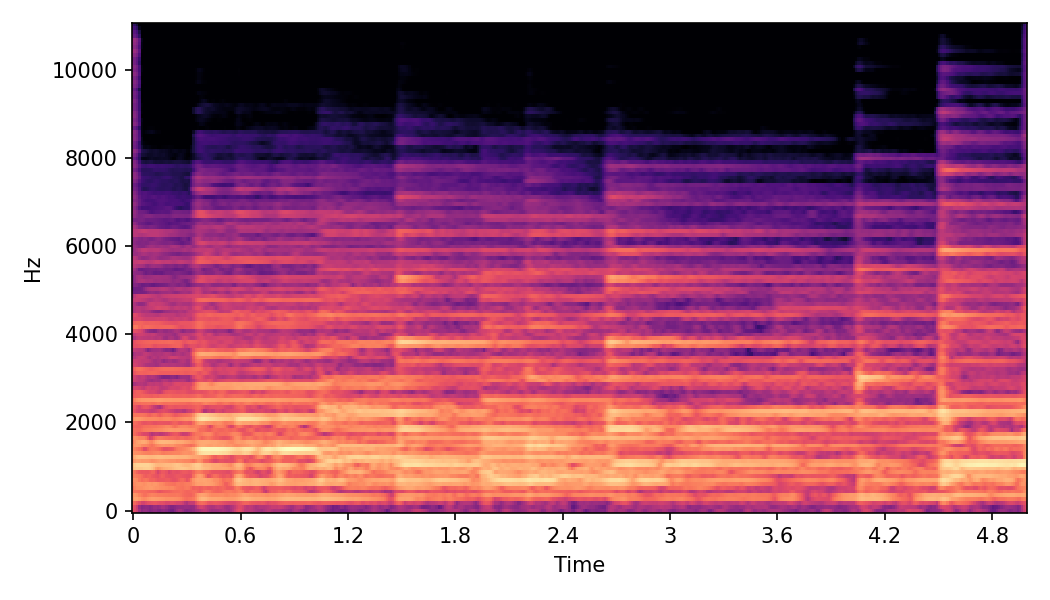
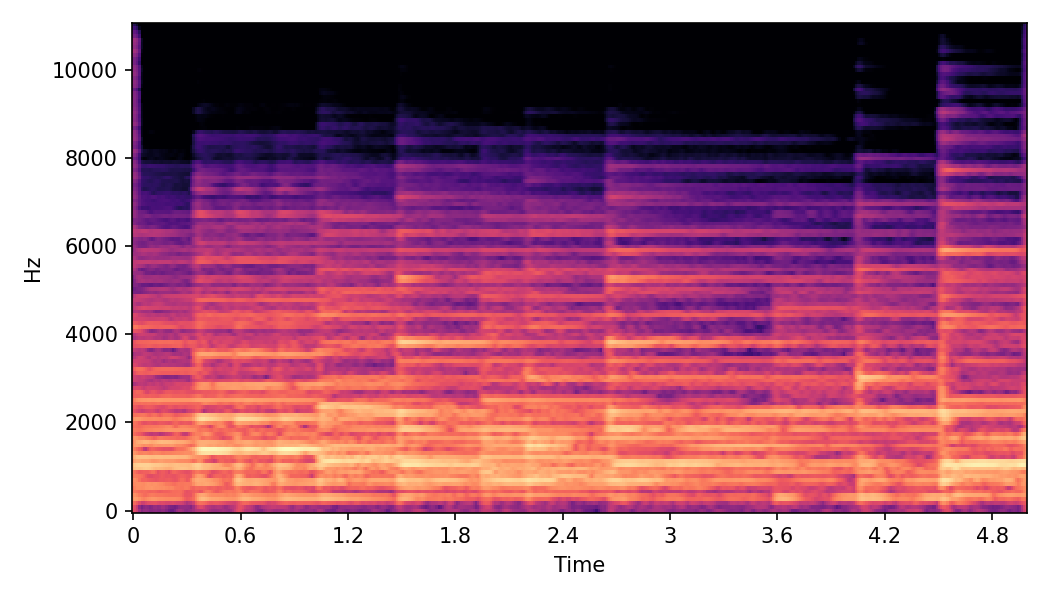
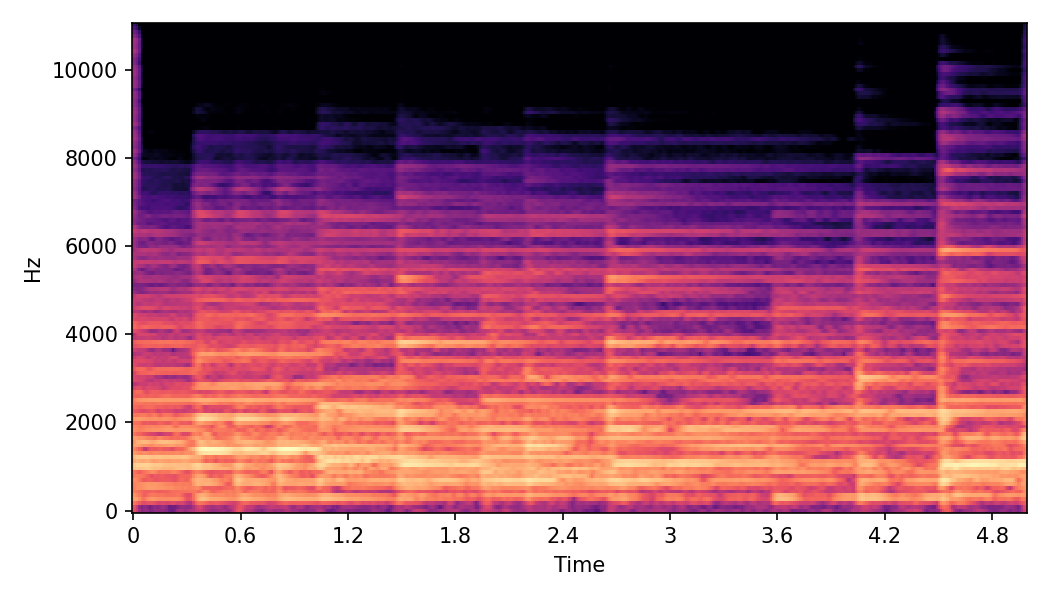
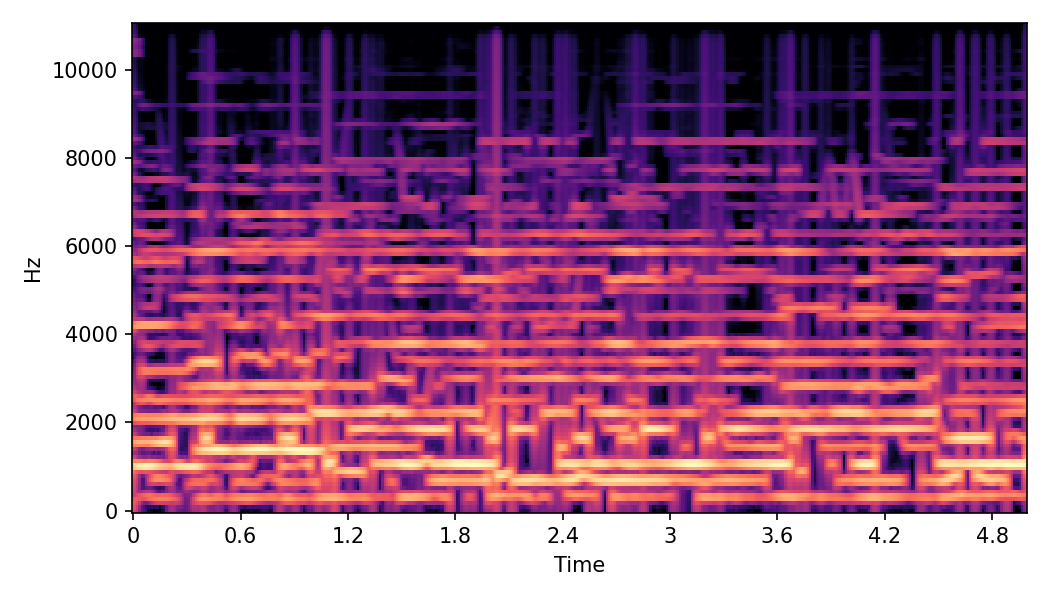
This page contains demonstration of timbre morphing for musical instruments comparison with SMT [1]. SMT is a MATLAB based timbre morphing technique that performs isolate musical instrument morphing. The source and target music samples are sourced from MusicMagus and Timberer.


Note:

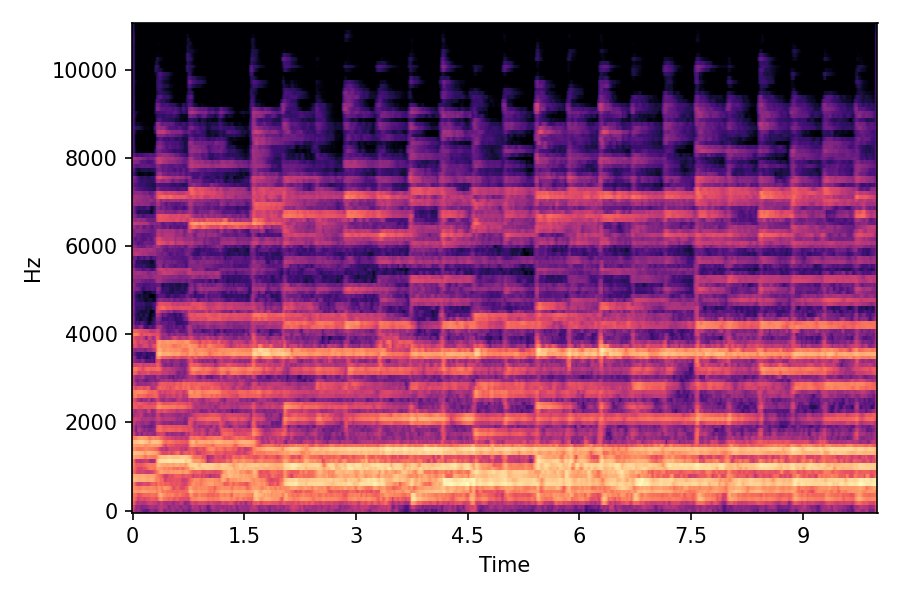
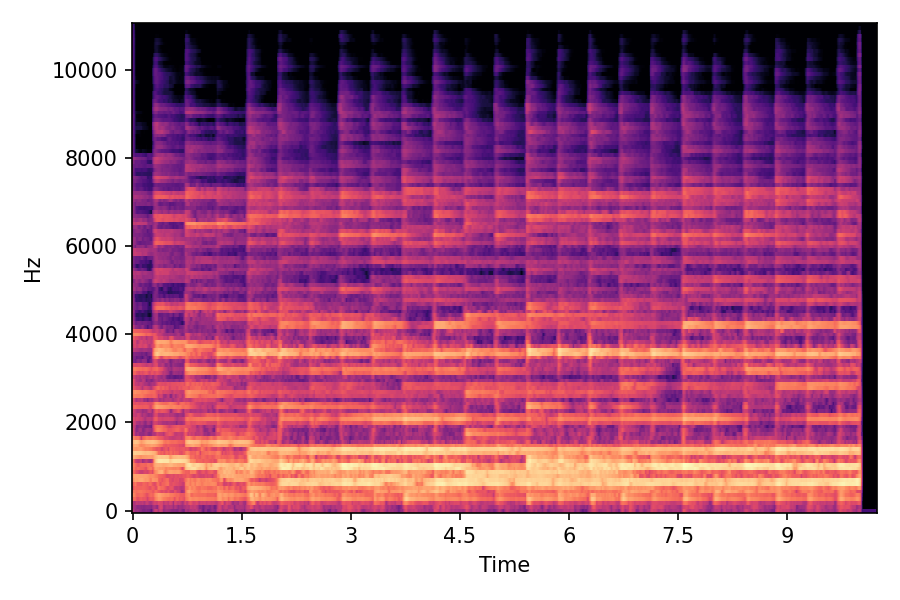
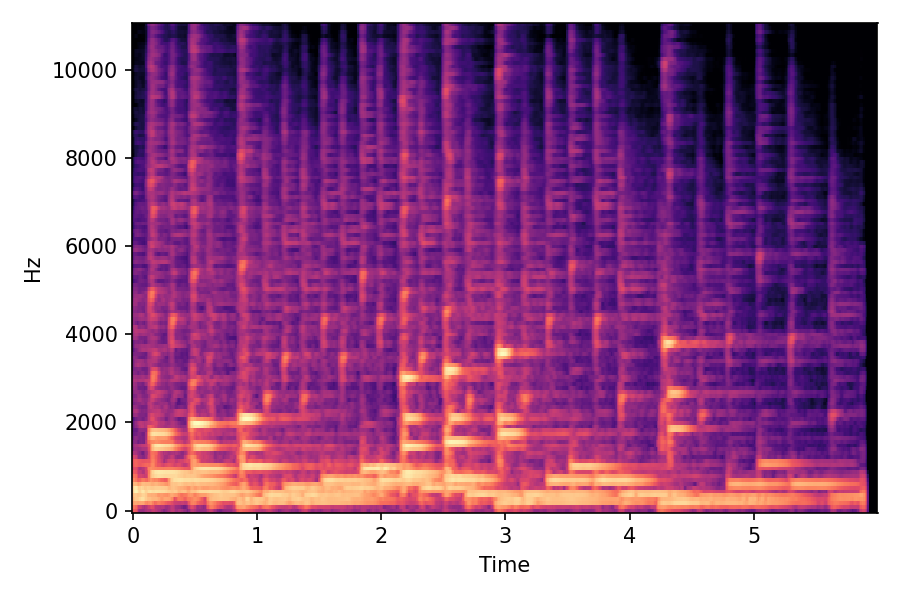
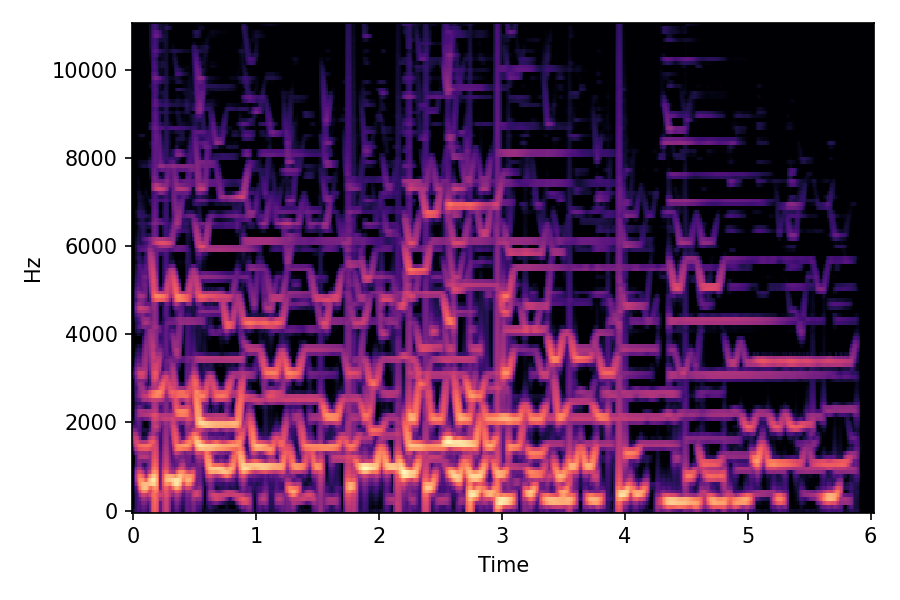
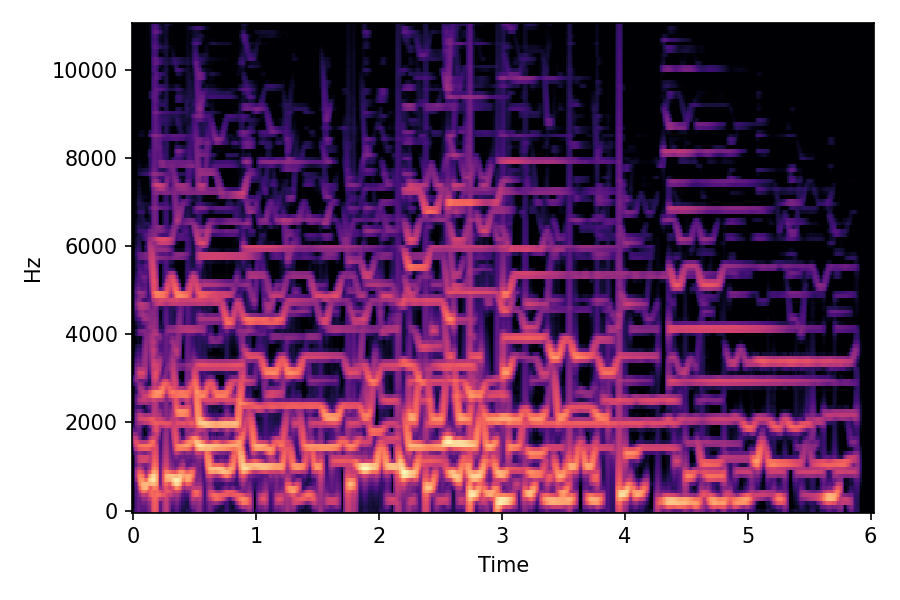
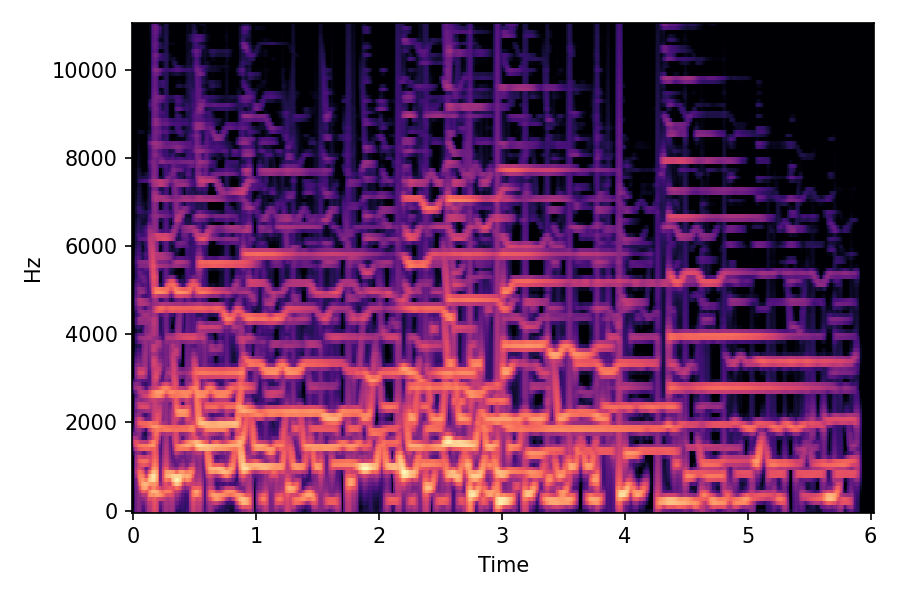
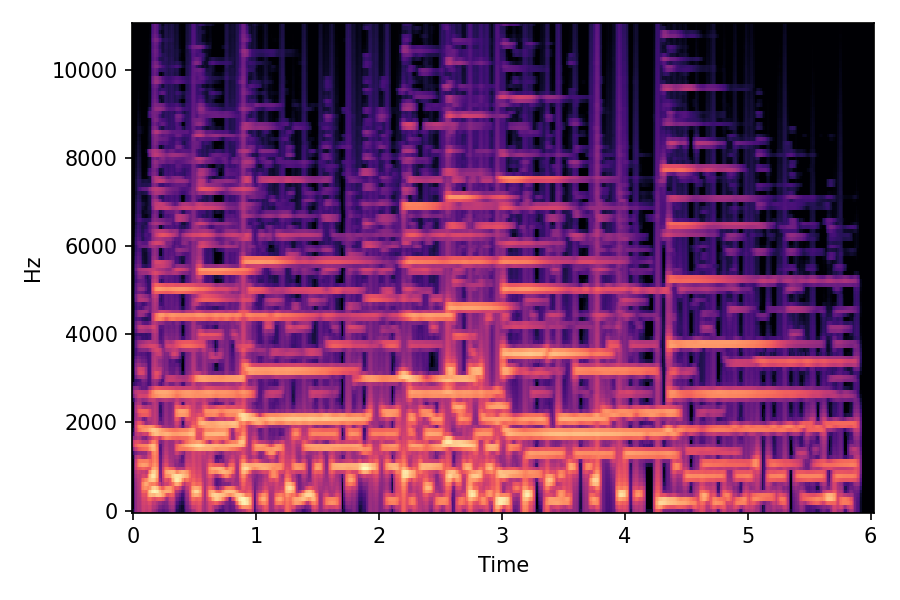
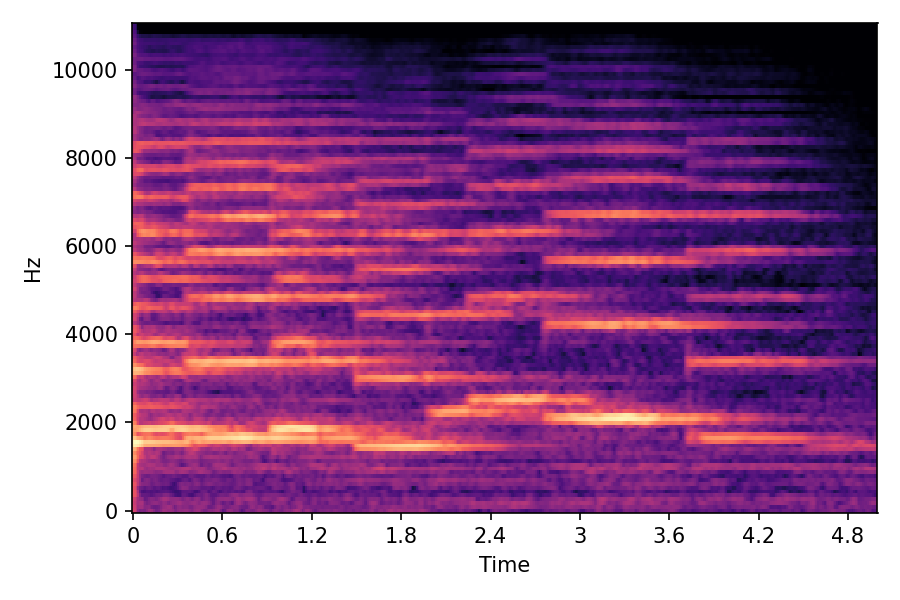
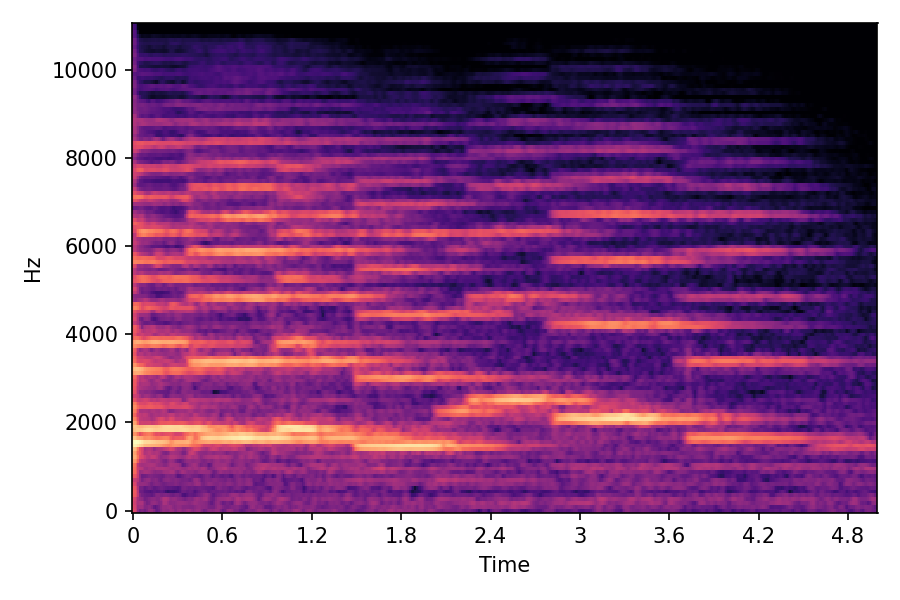
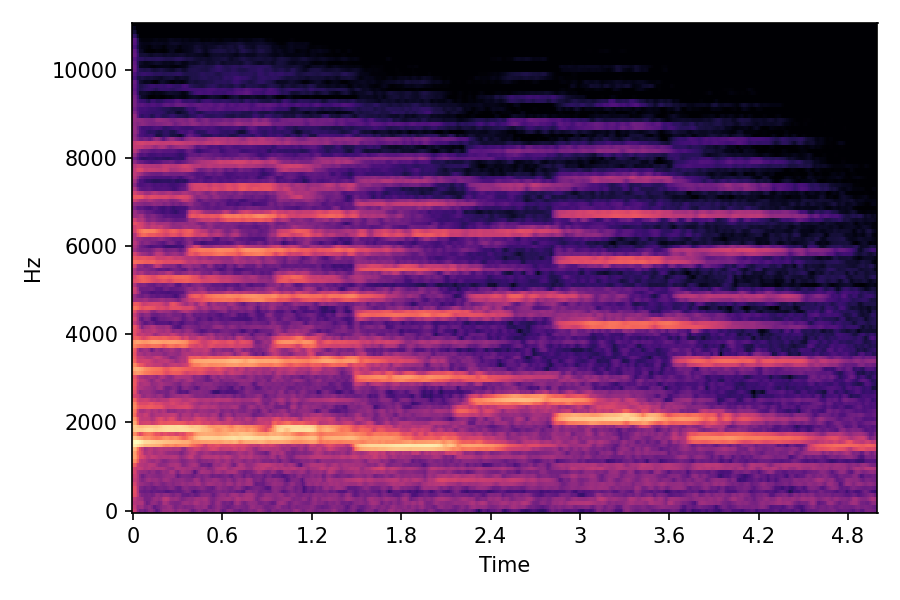
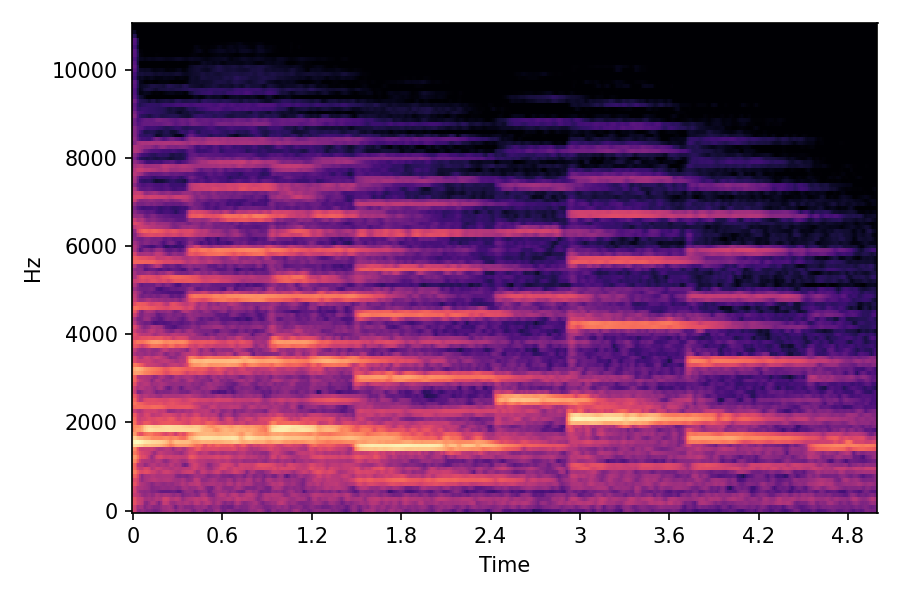
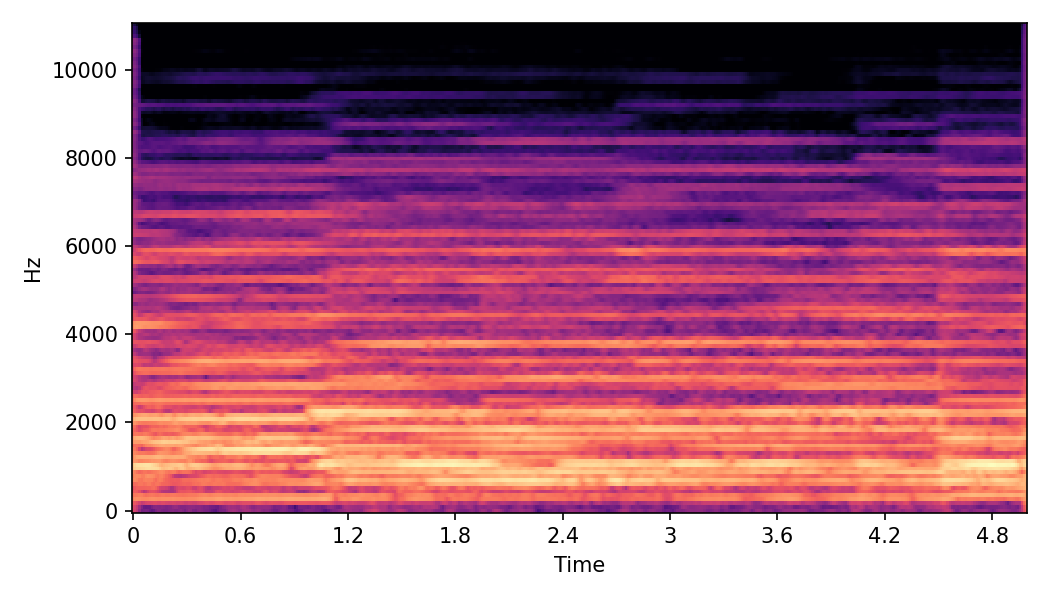
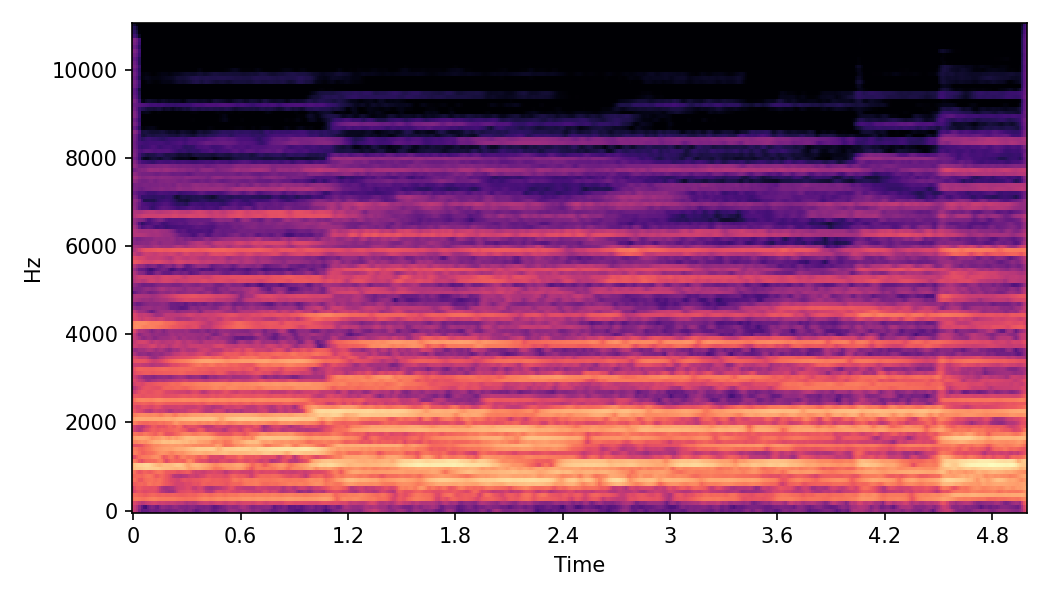
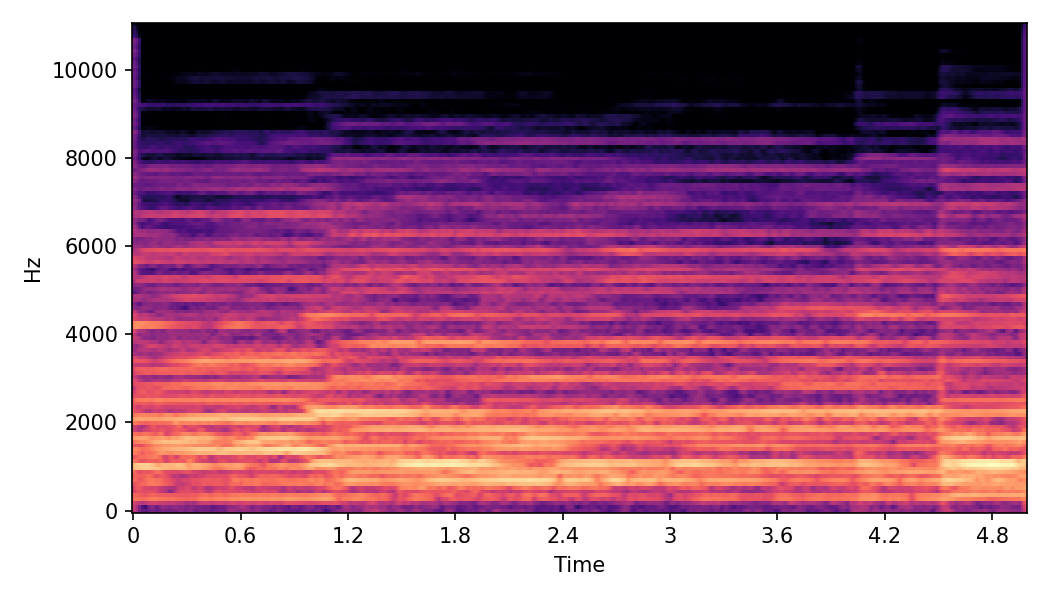
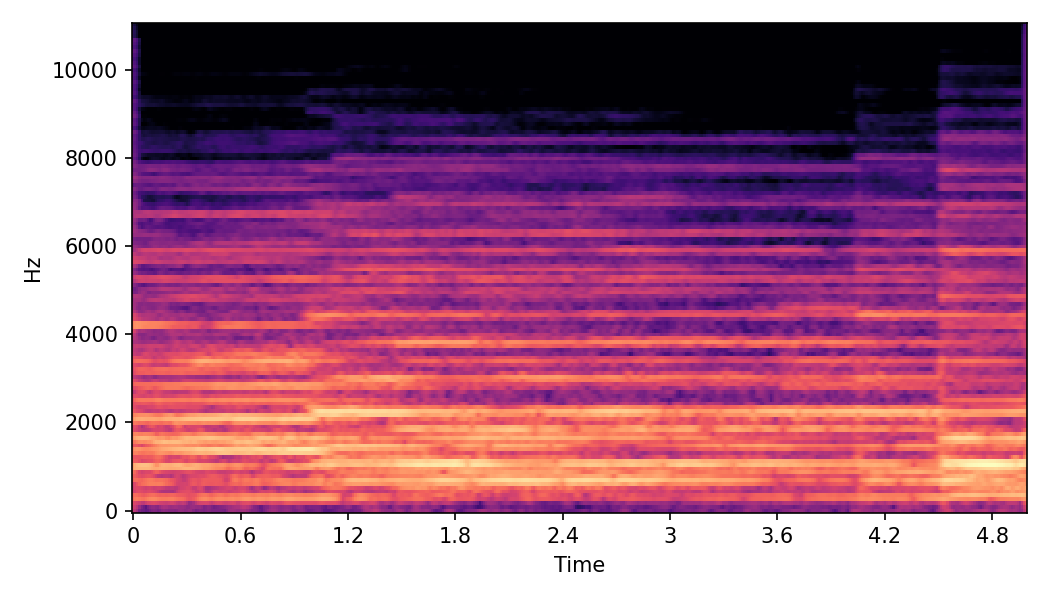
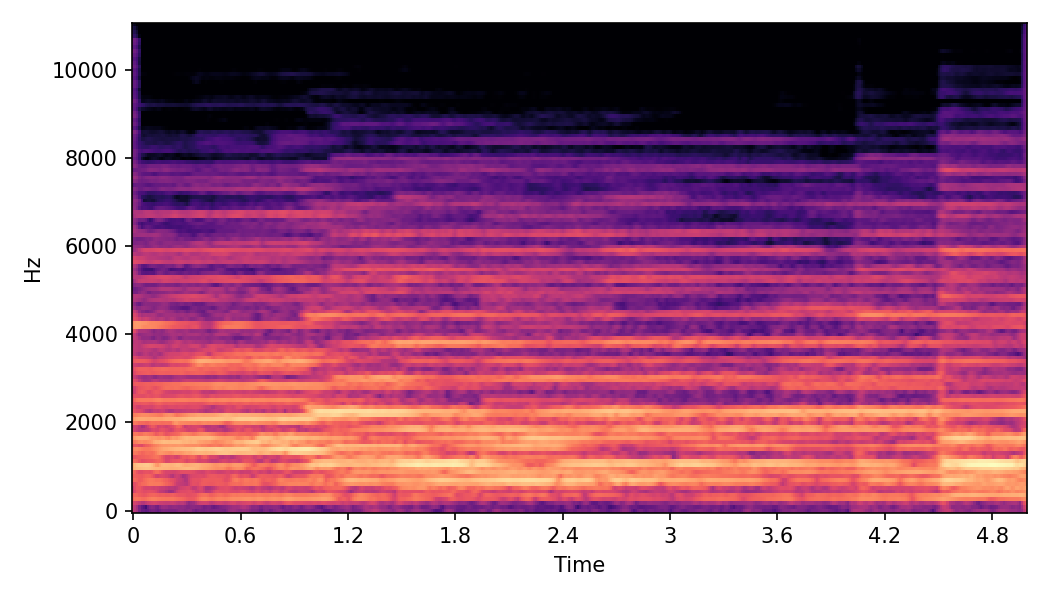
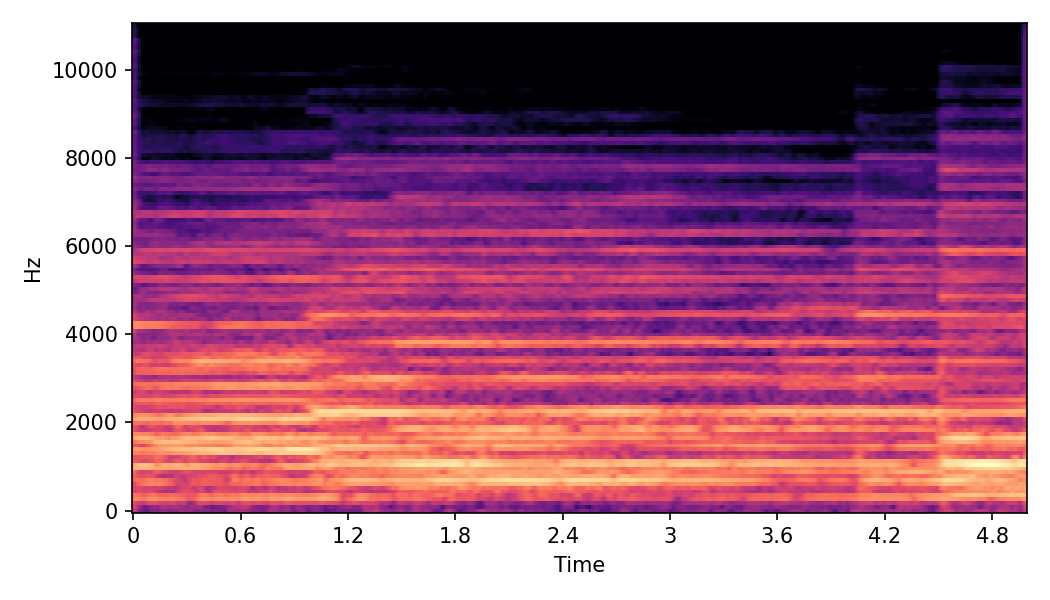
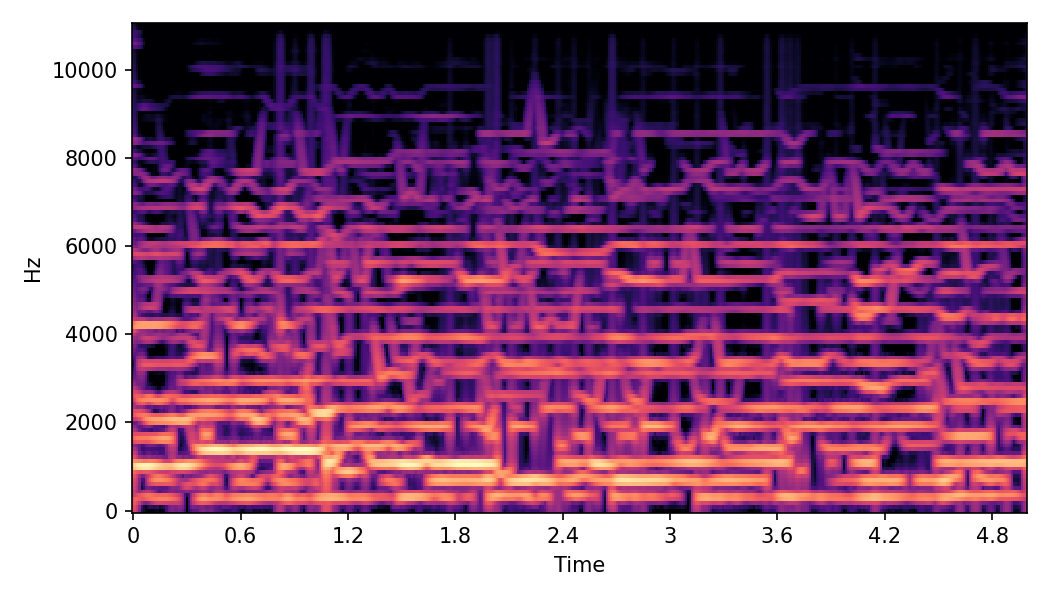
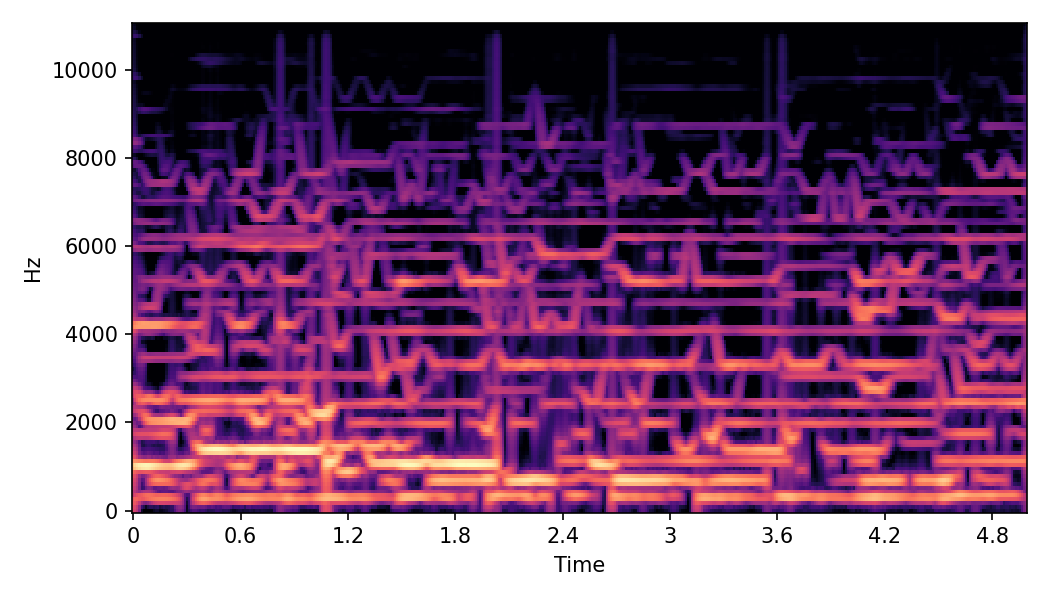
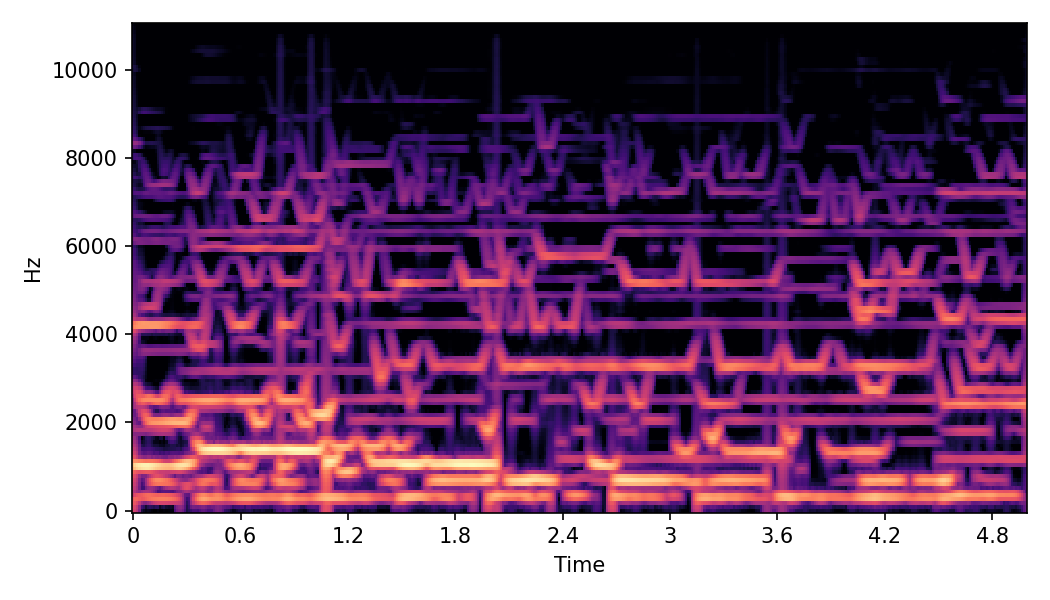
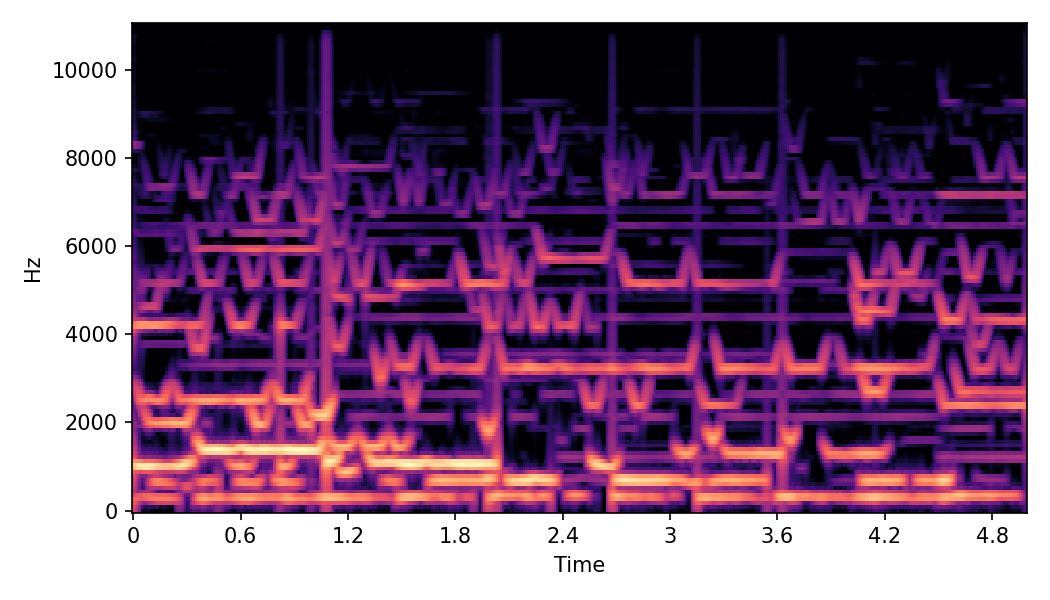
In SoundMorpher, samples morphs from a source audio (e.g., α =0.0) to target audio (e.g., α = 1.0). The audio samples are generated by morphing with a constant SPDP differences with Δ𝑝 = 0.1.

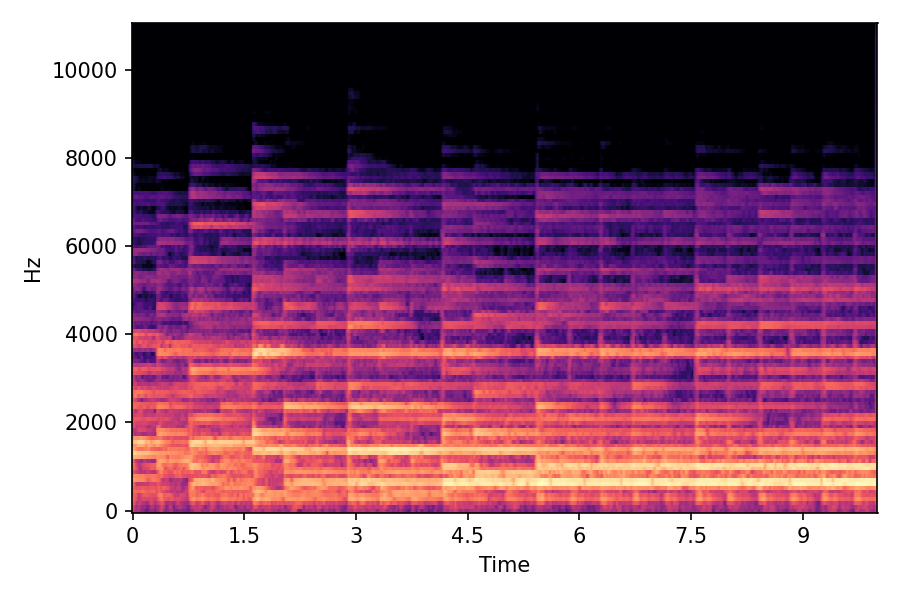
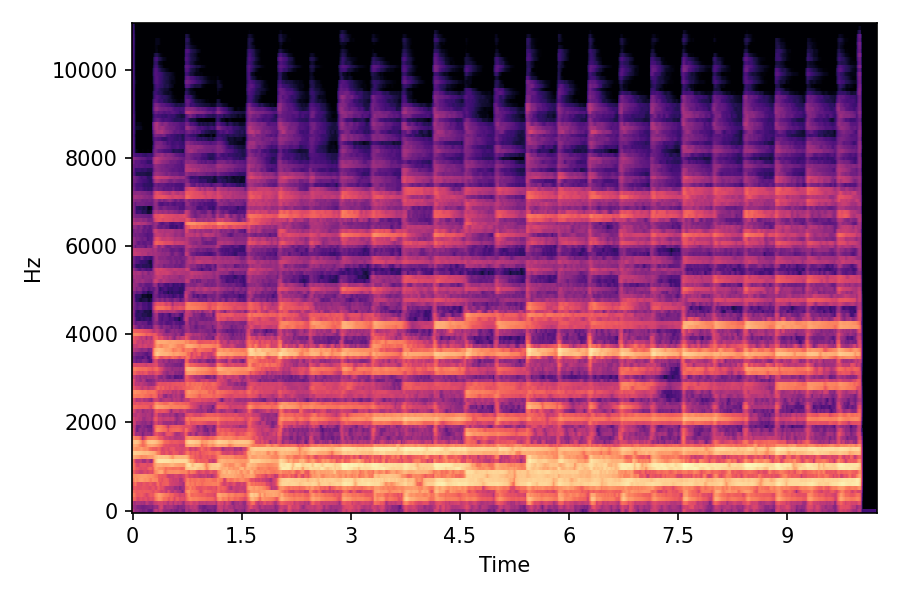
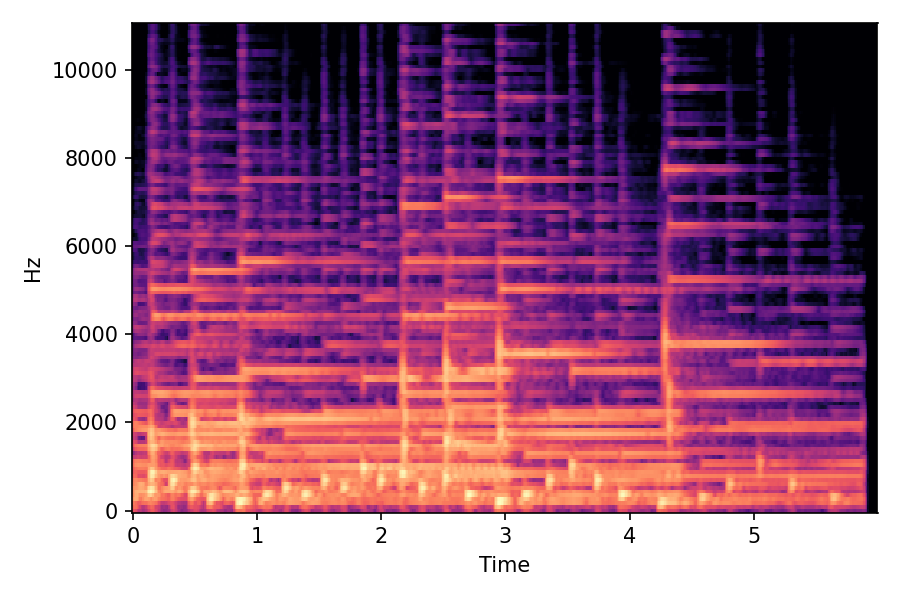
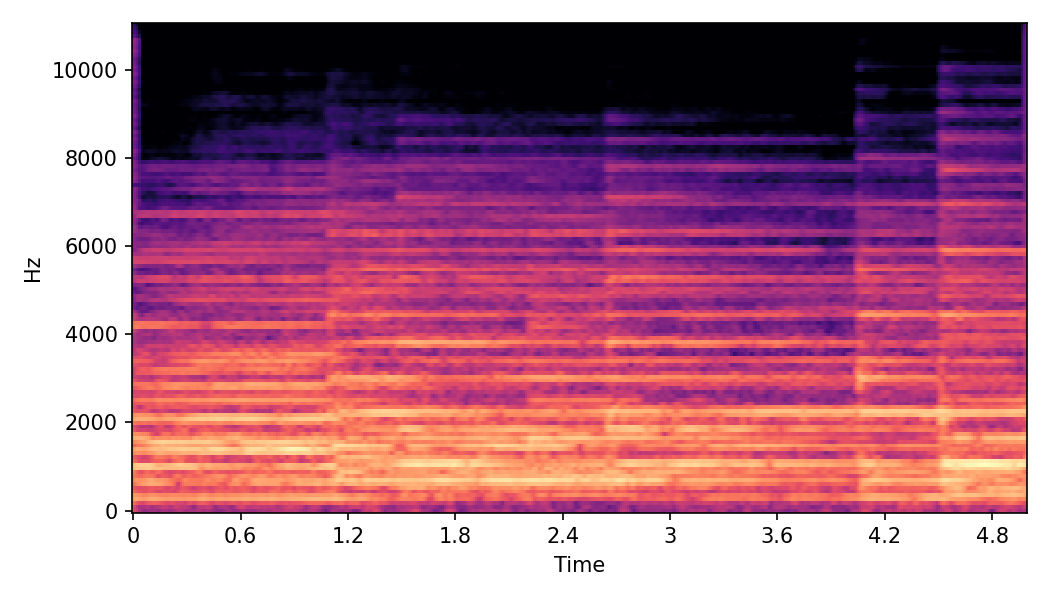
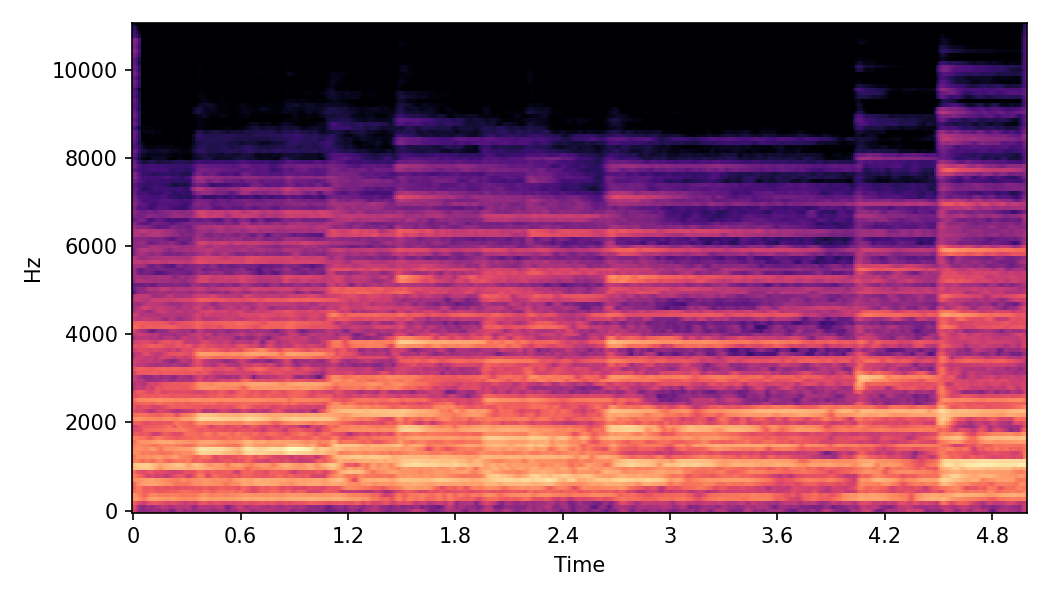
In SMT, the audio samples are generated by morphing with a constant morph factor differences in steps of Δα = 0.1.

Example 1

Source audio (Guitar)

Spectrogram α=0.0

Target audio (Piano)

Spectrogram α=0.25






SoundMorpher

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

SMT

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

Example 2

Source audio (Kalimaba)

Spectrogram α=0.0

Target audio (Harp)

Spectrogram α=0.25






SoundMorpher

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

SMT

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

Example 3

Source audio (Violin)

Spectrogram α=0.0

Target audio (Piano)

Spectrogram α=0.25






SoundMorpher

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

SMT

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

Example 4

Source audio (Guitar)

Spectrogram α=0.0

Target audio (Piano)

Spectrogram α=0.25






SoundMorpher

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

SMT

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

Example 5

Source audio (Organ)

Spectrogram α=0.0

Target audio (Piano)

Spectrogram α=0.25






SoundMorpher

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0

SMT

α=0.0

Spectrogram α=0.0


Spectrogram α=0.25


Spectrogram α=0.5


Spectrogram α=0.75


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0


Spectrogram α=1.0

α=1.0

Spectrogram α=1.0
Return index page

Reference

[1] Marcelo Caetano. Morphing musical instrument sounds with the sinusoidal model in the sound morphing toolbox. In International Symposium on Computer Music Multidisciplinary Research, pp. 481–503. Springer, 2019.